Цель: показать применение метода математической индукции для доказательства формул и решения задач на делимость.
Ход занятия
1. Вспомним, в чем же состоит суть метода математической индукции?
Доказательство методом математической индукции состоит из двух частей:
доказать или проверить справедливость утверждения при n =1;
предположить, что утверждение справедливо для n
=k ,где k 
N, и
доказать справедливость утверждения для n =k+1.
2.Доказательство формулы n -го члена арифметической прогрессии
a
= a
+ (n-1)d
В 9 классе эту формулу получили, увидев следующую закономерность:
а
= a
+ d
a
= a+ d = a+2d
a
= a+ d = a+3d и т. д.
То есть от частных утверждений пришли к общему выводу.
Но мы знаем, что если утверждение справедливо в целом ряде частных случаев, оно может быть несправедливо вообще.
(На предыдущем занятии рассматривали такой
пример, когда значение трехчлена x
+ x + 41 при x = 0,1,2,…39 является
простым числом, а при x = 40 40
+ 40 + 41 = 41 - составное число.)
Итак, доказательство:
1) n = 1 a= a - верно.
2) n = k a
= a + (k-1)d , докажем
справедливость формулы при n =k+1,то есть формула
должна выглядеть следующим образом a 
= a + (k + 1-1)d = a + kd.
По определению арифметической прогрессии a =a
+ d= a + (k-1)d + d = a+ d(k-1+1) = a + kd. Таким образом, формула доказана
(доказательство выполняется учеником).
3. Перейдем к задачам на делимость.
На доске восстанавливается треугольник Паскаля (работает ученик)
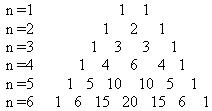
Пока восстанавливается треугольник Паскаля, с помощью формул сокращенного умножения раскрываются скобки в первых двух выражениях, в следующих двух пользуемся коэффициентами из треугольника:
(a + b)
=
(k + 1) =
(a + b)
=
(k + 1)
=
Предлагаются задачи на делимость:
а) доказать, что число n- n 
n
N
делится на 3;
б) доказать, что число n - n nN делится на 5;
в) доказать, что nN
число 3
+2
делится на 7;
г) доказать, что nN
число 11
+12
делится на 133.
Решение:
б) 1) при n =1 1-1=0,
0 делится на 5.
2) пусть при n =k k
-k делится на 5,тогда при n =k+1
(k+1)- (k+1) = k+ 5k
+ 10 k+ 10k
+ 5k + 1- k - 1=
k- k + 5k+ 10 k+ 10k+ 5k = (k- k) + 5(k+ 2 k+
2k+ k) кратно 5,
так как каждое слагаемое кратно 5.
Утверждения в задачах а), б) верны. Лейбниц одно время считал, что любое число вида
n 
- n , где k
=1,2,3,… делится на число (2k+1). Однако позже сам
обнаружил, что 2
- 2 не делится на 9.
Еще один пример. Ферма пришел к выводу, что
числа вида 2
+ 1
– простые и проверил справедливость вывода для n
=0,1,2,3,4. А в 1732 году Эйлер доказал, что число 2
+ 1 = 4294967297 –
составное, так как делится на 641.
в) 1) при n =1 3
+2
= 27 +8 = 35, 35
делится на 7.
2) пусть при n =k 3
+2
делится на 7, тогда при n =k+1
3
+2
= 3
+2
= 3•3+ 2·2 = 9•3 +2•2
=
2(3+2) + 7·3 делится на 7,
так как каждое слагаемое делится на 7.
г) решается аналогично в).
4. Итог занятия. Сегодня с помощью метода математической индукции определяли делимость чисел и еще раз убедились в том, что нельзя делать общий вывод (без доказательства) на основании справедливости частных утверждений.