В последнее время все чаще в поле зрения попадают задачи, в которых проводятся действия с обратными тригонометрическими функциями (аркфункциями). К таким задачам относятся и уравнения, содержащие эти функции.
Важным моментом при решении задач, содержащих обратные тригонометрические функции является следующее утверждение: “Если функция y=f(x) непрерывна и строго монотонна на некотором интервале, то она не может принимать одинаковые значения в различных точках интервала, а, следовательно, для любых х1,х2 из этого интервала из равенства f(x1)= f(x2) следует равенство х1=х2”.
В дальнейшем, наряду с формулами тригонометрии, будем пользоваться тождествами и соотношениями между обратными тригонометрическими функциями.
Прежде чем приступить к решению уравнений, содержащих обратные тригонометрические функции, следует обратить внимание на решение задач, в которых требуется проверить, имеет ли место заданное равенство.
Пример 1. Проверить, имеет ли место
равенство 
Решение. Обозначим  .
.
Требуется проверить равенство 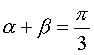 .
.
Так как 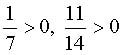 ,
то
,
то 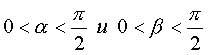 ,
следовательно
,
следовательно ![]() .
.
Учитывая, что ![]() для
для ![]() , найдем
, найдем ![]() .
.

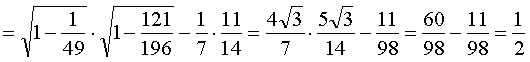
Итак,  . Так как функция cos x
непрерывна и строго монотонна на промежутке
. Так как функция cos x
непрерывна и строго монотонна на промежутке ![]() и
на нем принимает значение, равное 0,5, только при
и
на нем принимает значение, равное 0,5, только при  ,
то получим, что
,
то получим, что 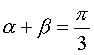 , то есть
, то есть  .
.
Следует заметить, что если находить не ![]() , а
, а ![]() , то
получим
, то
получим  , но функция sin x на
промежутке
, но функция sin x на
промежутке ![]() кусочно-монотонна и,
следовательно, из равенства
кусочно-монотонна и,
следовательно, из равенства  нельзя заключить,
что
нельзя заключить,
что 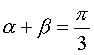 .
.
Действительно, наряду с  и
и  , причем
, причем  .
.
Пример 2. Доказать, что  .
.
Решение. Обозначим  . Требуется
доказать, что
. Требуется
доказать, что 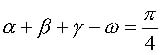 .
.
Так как 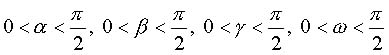 , а значит
, а значит 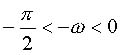 , то
, то  . На интервале
. На интервале  функции sin x,
cos x непрерывны и кусочно-монотонны,
следовательно, из равенства
функции sin x,
cos x непрерывны и кусочно-монотонны,
следовательно, из равенства  или
или  нельзя
сделать вывод, что
нельзя
сделать вывод, что 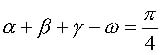 . Функция tg x на интервале
. Функция tg x на интервале  не
является непрерывной и из равенства
не
является непрерывной и из равенства 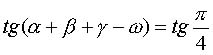 может
следовать
может
следовать 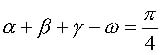 или
или  (аналогичный результат
получается, если рассматривать функцию ctg x).
Таким образом, возникла необходимость сузить
интервал, которому принадлежит аргумент
(аналогичный результат
получается, если рассматривать функцию ctg x).
Таким образом, возникла необходимость сузить
интервал, которому принадлежит аргумент ![]() .
Для этого оценим значения
.
Для этого оценим значения ![]() , учитывая известные
значения обратных тригонометрических функций, а
также тот факт, что функция arccos x
является убывающей на промежутке
, учитывая известные
значения обратных тригонометрических функций, а
также тот факт, что функция arccos x
является убывающей на промежутке ![]() , а функция arctg
x – возрастающей на промежутке
, а функция arctg
x – возрастающей на промежутке ![]() . Итак,
. Итак, 

 а
значит
а
значит  ;
;  . Тогда
. Тогда  ,
следовательно
,
следовательно  . На этом интервале функция tg x
непрерывна и строго монотонна, следовательно,
если взять тангенс от обеих частей исходного
уравнения и доказать, что
. На этом интервале функция tg x
непрерывна и строго монотонна, следовательно,
если взять тангенс от обеих частей исходного
уравнения и доказать, что 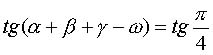 , то тем самым докажем, что
, то тем самым докажем, что 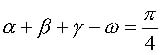 .
.
Используя формулы  , вычислим
, вычислим ![]() , а затем
, а затем ![]() по формуле
по формуле 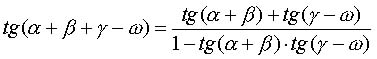 .
.
Итак, 
 ,
,

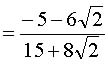 , тогда
, тогда 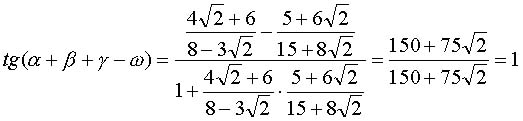 .
.
А так как и  , то
, то 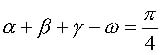 , то есть
, то есть  .
.
Решая уравнения, содержащие аркфункции, часто
сравнивают тригонометрические функции от обеих
частей данного уравнения. При этом новое
уравнение является следствием исходного, то есть
могут появиться посторонние корни, для выявления
которых необходима проверка. При проверке
требуется доказать или опровергнуть получаемые
равенства, содержащие значения обратных
тригонометрических функций, то есть решать
задачи, аналогичные рассмотренным в примерах 1, 2.
Следует также помнить, что функции tg x, ctg x
определены не для всех значений х, поэтому
при переходе от уравнения ![]() к уравнениям
к уравнениям ![]() может
произойти потеря решений.
может
произойти потеря решений.
При решении уравнений можно придерживаться следующей схемы:
найти область допустимых значений (ОДЗ) переменной, входящей в уравнение;
решить исходное уравнение, убедиться, что полученные решения входят в ОДЗ;
выполнить проверку, если в процессе решение сравнивались тригонометрические функции от обеих частей уравнения или в результате преобразований переходили к новому уравнению, являющемуся следствием данного.
Следует заметить, что иногда, находя промежутки, которым принадлежат аркфункции, входящие в уравнение, можно сделать вывод о существовании решения уравнения (примеры 3, 4).
Пример 3. Решить уравнение ![]() .
.
Решение. Так как  для любых действительных
значений х, а
для любых действительных
значений х, а ![]() не принадлежит этому промежутку,
то исходное уравнение не имеет решения.
не принадлежит этому промежутку,
то исходное уравнение не имеет решения.
Пример 4. Решить уравнение  .
.
Решение. ОДЗ: ![]() . Обозначим
. Обозначим  ;
;  ,
то есть заданное уравнение не имеет решения.
,
то есть заданное уравнение не имеет решения.
Пример 5. Решить уравнение  .
.
Решение. ОДЗ: ![]() . Здесь
. Здесь 
 ,
то есть уравнение может иметь решение.
Преобразуем уравнение, учитывая, что
,
то есть уравнение может иметь решение.
Преобразуем уравнение, учитывая, что 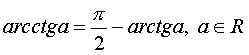 .
.

Возьмем тангенс от обеих частей уравнения и,
воспользовавшись тем, что ![]() , решим полученное
уравнение
, решим полученное
уравнение

х=1 не принадлежит ОДЗ, следовательно, является посторонним корнем.
Проверим, будет ли х=0 корнем исходного уравнения, подставив это значение в уравнение:

Следовательно, х = 0 является решением исходного уравнения.
Переходя к уравнению  мы могли потерять те
корни, для которых
мы могли потерять те
корни, для которых  не существует, то есть,
для которых
не существует, то есть,
для которых  . Решая это уравнение и учитывая,
что для
. Решая это уравнение и учитывая,
что для  , придем к уравнению
, придем к уравнению

которое не имеет решения. Следовательно, х = 0 – единственный корень исходного уравнения.
Пример 6. Решить уравнение  .
.
Решение. ОДЗ:  Возьмем синус от обеих
частей уравнения и, учитывая, что
Возьмем синус от обеих
частей уравнения и, учитывая, что ![]() , где
, где ![]() ,
решим полученное уравнение
,
решим полученное уравнение

Проверим, будет ли  решением исходного
уравнения, то есть проверим, будет ли иметь место
равенство
решением исходного
уравнения, то есть проверим, будет ли иметь место
равенство 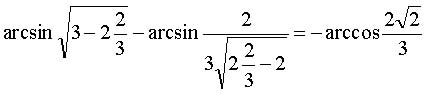 , то есть
, то есть 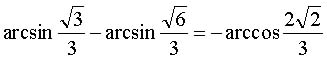 . Обозначим
. Обозначим  . Так как
функция arcsin t возрастающая, а arccos t
убывающая на промежутке
. Так как
функция arcsin t возрастающая, а arccos t
убывающая на промежутке ![]() , следовательно,
, следовательно,  , то есть
, то есть  ;
;  .
Таким образом
.
Таким образом  , а на этом промежутке функция sin t
непрерывна, строго монотонна и при этом
, а на этом промежутке функция sin t
непрерывна, строго монотонна и при этом  .
Следовательно,
.
Следовательно, ![]() , то есть равенство
, то есть равенство 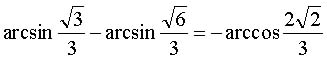 справедливо. А это и
означает, что
справедливо. А это и
означает, что  - единственный корень исходного
уравнения.
- единственный корень исходного
уравнения.
В ряде случаев, анализируя условия, определяющие область допустимых значений переменной, входящей в уравнение, содержащее аркфункции, данное уравнение сводится к проверке истинности получаемого при этом равенства.
Пример 7. Решить уравнение ![]() .
.
Решение. ОДЗ: ![]() , то есть
, то есть ![]() . Значит,
область допустимых значений переменной х
содержит только одну точку х = 2.
. Значит,
область допустимых значений переменной х
содержит только одну точку х = 2.
Подставим это значение в исходное уравнение и проверим, будет ли истинно полученное равенство, то есть, будет ли х = 2 решением уравнения.

Так как для ![]() , следовательно
, следовательно ![]() , а значит х
= 2 не является решением исходного уравнения
, а значит х
= 2 не является решением исходного уравнения ![]() .
.